線形回帰の場合,切片,a2,をシフト,したらどのような計算式になるのか?
・切片を変化させたときの残差平方和
\(\Large \displaystyle y_i = a_0 + a_1 x_i \)
a0をシフトさせたときの残差の平方和は,
\(\Large \displaystyle \sum_{i=1}^{n} \left( y_i -\hat{a_0} - a_1 x_i \right)^2 \)
であり,これが最小になる,\(\Large \displaystyle \hat{a_0} \),を計算すればいいので,
傾きの値a0を,δ,だけシフトさせて,固定し,その際のa1の推定値をソルバーで推定しました.
a0の標準誤差も加えてあります.
dS,を見ていただけるとわかるように,推定値,Seが一番小さく,左右対称に増加していることがわかります.
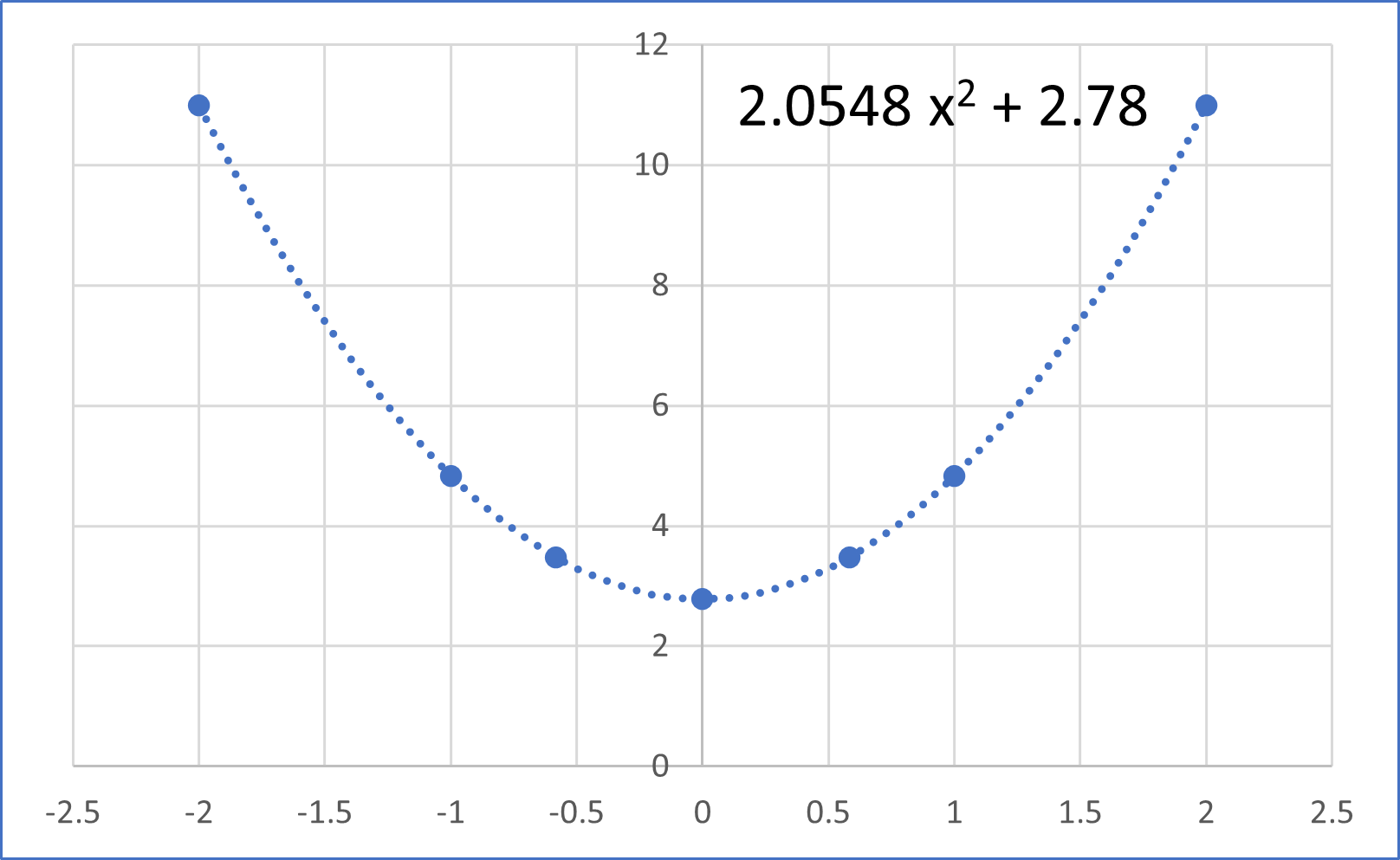
グラフ化すると,

のように,二乗+定数できれいに近似できます(xの項があるのはエクセルでべき乗で近似したため...)
ここで,分散値は,
・分散
\(\Large \displaystyle Ve = \frac{1}{n-2} \sum_{i=1}^{n} \left(y_i -\hat{a_0} - \hat{a_1} x_i \right)^2 = \frac{Se}{n-2} = \frac{2.78}{6-2} = 0.695 \)
であり(a0,a1,の二つのパラメータが2つあるので,自由度は,n-2),平均値の議論では,
\(\Large \displaystyle S_{SE} = Se + Ve \)
となり,当てはまりの悪さ,S,がSe + Ve,の場合のδが,標準誤差,SE,となるので,ちょうどa0のシフトが回帰分析で計算した標準誤差,±0.58157,の時に,Se+Ve,となります.
さて,実際にパラメータをシフトさせて残差平方和を求め,その結果が”二乗+定数”,となり,平均値の場合と同様の結果でしたが,これは偶然なのでしょうか?
それをきちんと計算してみましょう.しかし,とても面倒なので後回し,ここ,に記載します.
次に,二次曲線について考えていきましょう.